When the Jaccard similarity index isn’t the precise device for the job, and what to do as a substitute
I’ve been pondering these days about one in every of my go-to knowledge science instruments, one thing we use fairly a bit at Aampe: the Jaccard index. It’s a similarity metric that you just compute by taking the dimensions of the intersection of two units and dividing it by the dimensions of the union of two units. In essence, it’s a measure of overlap.
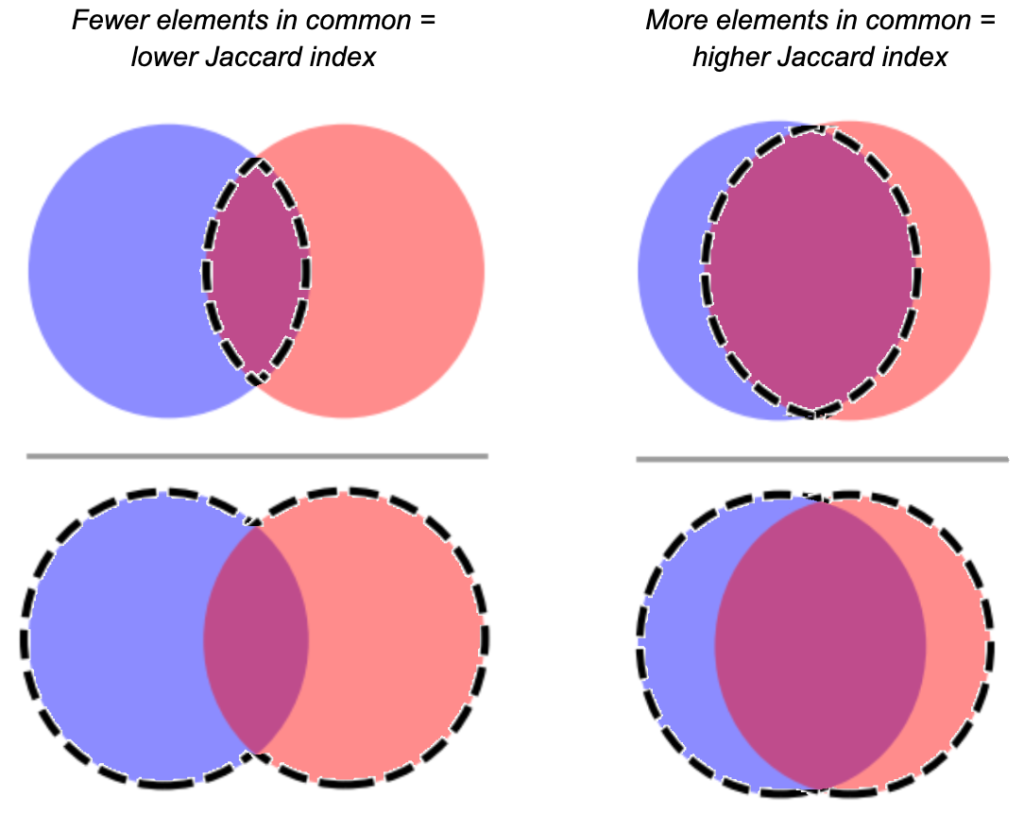
For my fellow visible learners:
Many (myself included) have sung the praises of the Jaccard index as a result of it is useful for lots of use instances the place you must determine the similarity between two teams of components. Whether or not you’ve received a comparatively concrete use case like cross-device identification decision, or one thing extra summary, like characterize latent consumer curiosity classes primarily based on historic consumer conduct — it’s actually useful to have a device that quantifies what number of parts two issues share.
However Jaccard just isn’t a silver bullet. Generally it’s extra informative when it’s used together with different metrics than when it’s used alone. Generally it’s downright deceptive.
Let’s take a more in-depth have a look at a number of instances when it’s not fairly applicable, and what you would possibly wish to do as a substitute (or alongside).
The issue: The larger one set is than the opposite (holding the dimensions of the intersection equal), the extra it depresses the Jaccard index.
In some instances, you don’t care if two units are reciprocally related. Perhaps you simply wish to know if Set A largely intersects with Set B.
Let’s say you’re attempting to determine a taxonomy of consumer curiosity primarily based on looking historical past. You have got a log of all of the customers who visited http://www.luxurygoodsemporium.com and a log of all of the customers who visited http://superexpensiveyachts.com (neither of that are dwell hyperlinks at press time; fingers crossed nobody creepy buys these domains sooner or later).
Say that out of 1,000 customers who browsed for tremendous costly yachts, 900 of them additionally appeared up some luxurious items — however 50,000 customers visited the posh items website. Intuitively, you would possibly interpret these two domains as related. Almost everybody who patronized the yacht area additionally went to the posh items area. Looks as if we is perhaps detecting a latent dimension of “high-end buy conduct.”
However as a result of the variety of customers who have been into yachts was a lot smaller than the variety of customers who have been into luxurious items, the Jaccard index would find yourself being very small (0.018) regardless that the overwhelming majority of the yacht-shoppers additionally browsed luxurious items!
What to do as a substitute: Use the overlap coefficient.
The overlap coefficient is the dimensions of the intersection of two units divided by the dimensions of the smaller set. Formally:
Let’s visualize why this is perhaps preferable to Jaccard in some instances, utilizing essentially the most excessive model of the issue: Set A is a subset of Set B.
When Set B is fairly shut in measurement to Set B, you’ve received an honest Jaccard similarity, as a result of the dimensions of the intersection (which is the dimensions of Set A) is near the dimensions of the union. However as you maintain the dimensions of Set A continuing and improve the dimensions of Set B, the dimensions of the union will increase too, and…the Jaccard index plummets.
The overlap coefficient doesn’t. It stays yoked to the dimensions of the smallest set. That implies that at the same time as the dimensions of Set B will increase, the dimensions of the intersection (which on this case is the entire measurement of Set A) will at all times be divided by the dimensions of Set A.
Let’s return to our consumer curiosity taxonomy instance. The overlap coefficient is capturing what we’re eager about right here — the consumer base for yacht-buying is linked to the posh items consumer base. Perhaps the web optimization for the yacht web site is not any good, and that’s why it’s not patronized as a lot as the posh items website. With the overlap coefficient, you don’t have to fret about one thing like that obscuring the connection between these domains.
Professional tip: if all you’ve got are the sizes of every set and the dimensions of the intersection, you’ll find the dimensions of the union by summing the sizes of every set and subtracting the dimensions of the intersection. Like this:
Additional studying: https://medium.com/rapids-ai/similarity-in-graphs-jaccard-versus-the-overlap-coefficient-610e083b877d
The issue: When set sizes are very small, your Jaccard index is lower-resolution, and typically that overemphasizes relationships between units.
Let’s say you’re employed at a start-up that produces cell video games, and also you’re growing a recommender system that implies new video games to customers primarily based on their earlier enjoying habits. You’ve received two new video games out: Mecha-Crusaders of the Cyber Void II: Prisoners of Vengeance, and Freecell.
A spotlight group most likely wouldn’t peg these two as being very related, however your evaluation reveals a Jaccard similarity of .4. No nice shakes, but it surely occurs to be on the upper finish of the opposite pairwise Jaccards you’re seeing — in spite of everything, Bubble Crush and Bubble Exploder solely have a Jaccard similarity of .39. Does this imply your cyberpunk RPG and Freecell are extra intently associated (so far as your recommender is anxious) than Bubble Crush and Bubble Exploder?
Not essentially. Since you took a more in-depth have a look at your knowledge, and solely 3 distinctive machine IDs have been logged enjoying Mecha-Crusaders, solely 4 have been logged enjoying Freecell, and a couple of of them simply occurred to have performed each. Whereas Bubble Crush and Bubble Exploder have been every visited by a whole bunch of gadgets. As a result of your samples for the 2 new video games are so small, a presumably coincidental overlap makes the Jaccard similarity look a lot greater than the true inhabitants overlap would most likely be.
What to do as a substitute: Good knowledge hygiene is at all times one thing to bear in mind right here — you’ll be able to set a heuristic to wait till you’ve collected a sure pattern measurement to contemplate a set in your similarity matrix. Like all estimates of statistical energy, there’s a component of judgment to this, primarily based on the everyday measurement of the units you’re working with, however keep in mind the final statistical finest apply that bigger samples are typically extra consultant of their populations.
However another choice you’ve got is to log-transform the dimensions of the intersection and the dimensions of the union. This output ought to solely be interpreted when evaluating two modified indices to one another.
Should you do that for the instance above, you get a rating fairly near what you had earlier than for the 2 new video games (0.431). However since you’ve got so many extra observations within the Bubble style of video games, the log-transformed intersection and log-transformed union are quite a bit nearer collectively — which interprets to a a lot larger rating.
Caveat: The trade-off right here is that you just lose some decision when the union has lots of components in it. Including 100 components to the intersection of a union with 1000’s of components may imply the distinction between a daily Jaccard rating of .94 and .99. Utilizing the log rework method would possibly imply that including 100 components to the intersection solely strikes the needle from a rating of .998 to .999. It will depend on what’s vital to your use case!
The issue: You’re evaluating two teams of components, however collapsing the weather into units ends in a lack of sign.
Because of this utilizing a Jaccard index to check two items of textual content just isn’t at all times an important thought. It may be tempting to take a look at a pair of paperwork and wish to get a measure of their similarity primarily based on what tokens are shared between them. However the Jaccard index assumes that the weather within the two teams to be in contrast are distinctive. Which flattens out phrase frequency. And in pure language evaluation, token frequency is commonly actually vital.
Think about you’re evaluating a ebook about vegetable gardening, the Bible, and a dissertation in regards to the life cycle of the white-tailed deer. All three of those paperwork would possibly embody the token “deer,” however the relative frequency of the “deer” token will fluctuate dramatically between the paperwork. The a lot larger frequency of the phrase “deer” within the dissertation most likely has a special semantic affect than the scarce makes use of of the phrase “deer” within the different paperwork. You wouldn’t desire a similarity measure to only neglect about that sign.
What to do as a substitute: Use cosine similarity. It’s not only for NLP anymore! (But in addition it’s for NLP.)
Briefly, cosine similarity is a approach to measure how related two vectors are in multidimensional area (regardless of the magnitude of the vectors). The path a vector goes in multidimensional area will depend on the frequencies of the scale which can be used to outline the area, so details about frequency is baked in.
To make it straightforward to visualise, let’s say there are solely two tokens we care about throughout the three paperwork: “deer” and “bread.” Every textual content makes use of these tokens a special variety of occasions. The frequency of those tokens change into the scale that we plot the three texts in, and the texts are represented as vectors on this two-dimensional aircraft. As an example, the vegetable gardening ebook mentions deer 3 occasions and bread 5 occasions, so we plot a line from the origin to (3, 5).
Right here you wish to have a look at the angles between the vectors. θ1 represents the similarity between the dissertation and the Bible; θ2, the similarity between the dissertation and the vegetable gardening ebook; and θ3, the similarity between the Bible and the vegetable gardening ebook.
The angles between the dissertation and both of the opposite texts is fairly massive. We take that to imply that the dissertation is semantically distant from the opposite two — no less than comparatively talking. The angle between the Bible and the gardening ebook is small relative to every of their angles with the dissertation, so we’d take that to imply there’s much less semantic distance between the 2 of them than from the dissertation.
However we’re speaking right here about similarity, not distance. Cosine similarity is a change of the angle measurement of the 2 vectors into an index that goes from 0 to 1*, with the identical intuitive sample as Jaccard — 0 would imply two teams don’t have anything in frequent, and nearer you get to 1 the extra related the 2 teams are.
* Technically, cosine similarity can go from -1 to 1, however we’re utilizing it with frequencies right here, and there may be no frequencies lower than zero. So we’re restricted to the interval of 0 to 1.
Cosine similarity is famously utilized to textual content evaluation, like we’ve finished above, however it may be generalized to different use instances the place frequency is vital. Let’s return to the posh items and yachts use case. Suppose you don’t merely have a log of which distinctive customers went to every website, you even have the counts of variety of occasions the consumer visited. Perhaps you discover that every of the 900 customers who went to each web sites solely went to the posh items website a couple of times, whereas they went to their yacht web site dozens of occasions. If we consider every consumer as a token, and subsequently as a special dimension in multidimensional area, a cosine similarity method would possibly push the yacht-heads somewhat additional away from the posh good patrons. (Observe that you would be able to run into scalability points right here, relying on the variety of customers you’re contemplating.)
Additional studying: https://medium.com/geekculture/cosine-similarity-and-cosine-distance-48eed889a5c4
I nonetheless love the Jaccard index. It’s easy to compute and usually fairly intuitive, and I find yourself utilizing it on a regular basis. So why write a complete weblog put up dunking on it?
As a result of nobody knowledge science device can provide you an entire image of your knowledge. Every of those completely different measures inform you one thing barely completely different. You will get precious data out of seeing the place the outputs of those instruments converge and the place they differ, so long as you realize what the instruments are literally telling you.
Philosophically, we’re in opposition to one-size-fits-all approaches at Aampe. After on a regular basis we’ve spent what makes customers distinctive, we’ve realized the worth of leaning into complexity. So we predict the broader the array of instruments you should use, the higher — so long as you understand how to make use of them.