EDA for Word Embeddings. | Towards Data Science

Visualizing sudden insights in textual content information

When beginning work with a brand new dataset, it’s all the time a good suggestion to start out with some exploratory information evaluation (EDA). Taking the time to know your information earlier than coaching any fancy fashions may also help you perceive the construction of the dataset, establish any apparent points, and apply domain-specific data.

You see EDA in numerous kinds with all the pieces from house prices to superior purposes within the information science trade. However I nonetheless haven’t seen it for the most well liked new dataset: phrase embeddings, the idea of our greatest massive language fashions. So why not attempt it?

On this article, we’ll apply EDA to GloVe phrase embeddings, utilizing strategies like covariance matrices, clustering, PCA, and vector math. This may assist us perceive the construction of phrase embeddings, giving us a helpful place to begin for constructing extra highly effective fashions with this information. As we uncover this construction, we’ll discover that it’s not all the time what it appears, and a few stunning biases are hidden within the corpus.

You will have:

• Fundamental understanding of linear algebra, statistics, and vector arithmetic
• Python packages: numpy, sklearn, and matplotlib
• About 3 GB of spare disk area

To get began, obtain the dataset at huggingface.co/stanfordnlp/glove/resolve/main/glove.6B.zip[1]. This incorporates three textual content information, every containing a listing of phrases together with their vector representations. We’ll use the 300-dimensional representations (glove.6B.300d.txt).

A fast be aware on the place this dataset comes from: primarily, this can be a listing of phrase embeddings derived from 6 billion tokens’ value of co-occurrence information from Wikipedia and numerous information sources. A helpful facet impact of utilizing co-occurrence is that phrases that imply comparable issues are usually shut collectively. For instance, since “the purple chook” and “the blue chook” are each legitimate sentences, we would count on the vectors for “purple” and “blue” to be shut to one another. For extra technical info, you possibly can test the original GloVe paper[1].

To be clear, these are not phrase embeddings skilled for the aim of enormous language fashions. They’re a completely unsupervised approach based mostly on a big corpus. However they show lots of comparable properties to language mannequin embeddings, and are attention-grabbing in their very own proper.

Every line of this textual content file consists of a phrase, adopted by all 300 vector elements of the related embedding separated by areas. We will load that in with Python. (To scale back noise and velocity issues up, I’m utilizing the highest 10% of the complete dataset right here with the //10, however you possibly can change that should you’d like.)

import numpy as np
embeddings = {}
with open(f"glove.6B/glove.6B.300d.txt", "r") as f:
glove_content = f.learn().break up('n')
for i in vary(len(glove_content)//10):
line = glove_content[i].strip().break up(' ')
if line[0] == '':
proceed
phrase = line[0]
embedding = np.array(listing(map(float, line[1:])))
embeddings[word] = embedding
print(len(embeddings))

That leaves us with 40,000 embeddings loaded in.

One pure query we would ask is: are vectors typically near different vectors with comparable which means? And as a follow-up query, how can we quantify this?

There are two essential methods we’ll quantify similarity between vectors: one is Euclidean distance, which is solely the pure Pythagorean theorem distance we’re conversant in. The opposite is cosine similarity, which measures the cosine of the angle between two vectors. A vector has a cosine similarity of 1 with itself, -1 with an reverse vector, and 0 with an orthogonal vector.

Let’s implement these in NumPy:

def cos_sim(a, b):
return np.dot(a,b)/(np.linalg.norm(a) * np.linalg.norm(b))
def euc_dist(a, b):
return np.sum(np.sq.(a - b)) # no want for sq. root since we're simply rating distances

Now we are able to discover all of the closest vectors to a given phrase or embedding vector! We’ll do that in growing order.

def get_sims(to_word=None, to_e=None, metric=cos_sim):
# listing all similarities to the phrase to_word, OR the embedding vector to_e
assert (to_word isn't None) ^ (to_e isn't None) # discover similarity to a phrase or a vector, not each
sims = []
if to_e is None:
to_e = embeddings[to_word] # get the embedding for the phrase we're 
for phrase in embeddings:
if phrase == to_word:
proceed
word_e = embeddings[word]
sim = metric(word_e, to_e)
sims.append((sim, phrase))
sims.kind()
return sims

Now we are able to write a operate to show the ten most comparable phrases. Will probably be helpful to incorporate a reverse choice as nicely, so we are able to show the least comparable phrases.

def display_sims(to_word=None, to_e=None, n=10, metric=cos_sim, reverse=False, label=None):
assert (to_word isn't None) ^ (to_e isn't None)
sims = get_sims(to_word=to_word, to_e=to_e, metric=metric)
show = lambda sim: f'{sim[1]}: {sim[0]:.5f}'
if label is None:
label = to_word.higher() if to_word isn't None else ''
print(label) # a heading so we all know what these similarities are for
if reverse:
sims.reverse()
for i, sim in enumerate(reversed(sims[-n:])):
print(i+1, show(sim))
return sims

Lastly, we are able to check it!

display_sims(to_word='purple')
# yellow, blue, pink, inexperienced, white, purple, black, coloured, sox, vibrant

Seems to be just like the Boston Crimson Sox made an sudden look right here. However aside from that, that is about what we’d count on.

Perhaps we are able to attempt some verbs, and never simply nouns and adjectives? How a couple of good and sort verb like “share”?

display_sims(to_word='share')
# shares, inventory, revenue, p.c, shared, earnings, earnings, value, achieve, cents

I assume “share” isn’t usually used as a verb on this dataset. Oh nicely.

We will attempt some extra standard examples as nicely:

display_sims(to_word='cat')
# canine, cats, pet, canine, feline, monkey, horse, pets, rabbit, leopard
display_sims(to_word='frog')
# toad, frogs, snake, monkey, squirrel, species, rodent, parrot, spider, rat
display_sims(to_word='queen')
# elizabeth, princess, king, monarch, royal, majesty, victoria, throne, girl, crown

One of many fascinating properties about phrase embeddings is that analogy is in-built utilizing vector math. The instance from the GloVe paper is king – queen = man – girl. In different phrases, rearranging the equation, we count on king = man – girl + queen. Is that this true?

display_sims(to_e=embeddings['man'] - embeddings['woman'] + embeddings['queen'], label='king-queen analogy')
# queen, king, ii, majesty, monarch, prince...

Not fairly: the closest vector to man – girl + queen seems to be queen (cosine similarity 0.78), adopted considerably distantly by king (cosine similarity 0.66). Impressed by this wonderful 3Blue1Brown video, we would attempt aunt and uncle as an alternative:

display_sims(to_e=embeddings['aunt'] - embeddings['woman'] + embeddings['man'], label='aunt-uncle analogy')
# aunt, uncle, brother, grandfather, grandmother, cousin, uncles, grandpa, dad, father

That is higher (cosine similarity 0.7348 vs 0.7344), however nonetheless doesn’t work completely. However we are able to attempt switching to Euclidean distance. Now we have to set reverse=True, as a result of a greater Euclidean distance is definitely a decrease similarity.

display_sims(to_e=embeddings['aunt'] - embeddings['woman'] + embeddings['man'], metric=euc_dist, reverse=True, label='aunt-uncle analogy')
# uncle, aunt, grandfather, brother, cousin, grandmother, newphew, dad, grandpa, cousins

Now we received it. Nevertheless it looks like the analogy math won’t be as excellent as we hoped, at the very least within the naïve approach that we’re doing it right here.

Cosine similarity is all in regards to the angles between vectors. However is the magnitude of a vector additionally necessary?

We will reuse our current code by expressing magnitude because the Euclidean distance from the zero vector. Let’s see which phrases have the biggest and smallest magnitudes:

zero_vec = np.zeros_like(embeddings['the'])
display_sims(to_e=zero_vec, metric=euc_dist, label='largest magnitude')
# republish, nonsubscribers, hushen, tael, www.star, stoxx, 202-383-7824, resend, non-families, 225-issue
display_sims(to_e=zero_vec, metric=euc_dist, reverse=True, label='smallest magnitude')
# likewise, lastly, curiously, satirically, by the way, furthermore, conversely, moreover, aforementioned, whereby

It doesn’t appear like there’s a lot of a sample to the which means of the big magnitude vectors, however all of them appear to have very particular (and generally complicated) meanings. Then again, the smallest magnitude vectors are usually quite common phrases that may be present in a wide range of contexts.

There’s a large vary between magnitudes: from about 2.6 for the smallest vector all the way in which to about 17 for the biggest. What does this distribution appear like? We will plot a histogram to get a greater image of this.

import matplotlib.pyplot as plt
def plot_magnitudes():
phrases = [w for w in embeddings]
magnitude = lambda phrase: np.linalg.norm(embeddings[word])
magnitudes = listing(map(magnitude, phrases))
plt.hist(magnitudes, bins=40)
plt.present()
plot_magnitudes()

This distribution appears roughly regular. If we needed to check this additional, we might use a Q-Q plot. However for our functions proper now, that is tremendous.

It seems that instructions and subspaces in vector embeddings can encode numerous sorts of ideas, usually in biased methods. This paper[2] studied how this works for gender bias.

We will replicate this idea in our GloVe embeddings, too. First, let’s discover the course of the idea of “masculinity”. We will accomplish this by taking the common of variations between vectors like he and she, man and girl, and so forth:

gender_pairs = [('man', 'woman'), ('men', 'women'), ('brother', 'sister'), ('he', 'she'),
('uncle', 'aunt'), ('grandfather', 'grandmother'), ('boy', 'girl'),
('son', 'daughter')]
masc_v = zero_vec
for pair in gender_pairs:
masc_v += embeddings[pair[0]]
masc_v -= embeddings[pair[1]]

Now we are able to discover the “most masculine” and “most female” vectors, as judged by the embedding area.

display_sims(to_e=masc_v, metric=cos_sim, label='masculine vecs')
# brother, colonel, himself, uncle, gen., nephew, brig., brothers, son, sir
display_sims(to_e=masc_v, metric=cos_sim, reverse=True, label='female vecs')
# actress, herself, businesswoman, chairwoman, pregnant, she, her, sister, actresses, girl

Now, we are able to run a straightforward check to detect bias within the dataset: compute the similarity between nurse and every of man and girl. Theoretically, these needs to be about equal: nurse isn’t a gendered phrase. Is that this true?

print("nurse - man", cos_sim(embeddings['nurse'], embeddings['man'])) # 0.24
print("nurse - girl", cos_sim(embeddings['nurse'], embeddings['woman'])) # 0.45

That’s a fairly large distinction! (Bear in mind cosine similarity runs from -1 to 1, with constructive associations within the vary 0 to 1.) For reference, 0.45 can be near the cosine similarity between cat and leopard.

Let’s see if we are able to cluster phrases with comparable which means utilizing ok-means clustering. That is simple to do with the package deal scikit-learn. We’re going to use 300 clusters, which seems like quite a bit, however belief me: nearly all the clusters are so attention-grabbing, you could possibly write a whole article simply deciphering them!

from sklearn.cluster import KMeans
def get_kmeans(n=300):
kmeans = KMeans(n_clusters=n, n_init=1)
X = np.array([embeddings[w] for w in embeddings])
kmeans.match(X)
return kmeans
def display_kmeans(kmeans):
# print all clusters and 5 related phrases for every
phrases = np.array([w for w in embeddings])
X = np.array([embeddings[w] for w in embeddings])
y = kmeans.predict(X) # get the cluster for every phrase
for cluster in vary(kmeans.cluster_centers_.form[0]):
print(f'KMeans {cluster}')
cluster_words = phrases[y == cluster] # get all phrases in every cluster
for i, w in enumerate(cluster_words[:5]):
print(i+1, w)
kmeans = get_kmeans()
display_kmeans(kmeans)

There’s quite a bit to have a look at right here. Now we have clusters for issues as numerous as New York Metropolis (manhattan, n.y., brooklyn, hudson, borough), molecular biology (protein, proteins, enzyme, beta, molecules), and Indian names (singh, ram, gandhi, kumar, rao).

However generally these clusters are usually not what they appear. Let’s write code to show all phrases of a cluster containing a given phrase, together with the closest and farthest cluster.

def get_kmeans_cluster(kmeans, phrase=None, cluster=None):
# given a phrase, discover the cluster of that phrase. (or begin with a cluster index.)
# then, get all phrases of that cluster.
assert (phrase is None) ^ (cluster is None)
if cluster is None:
cluster = kmeans.predict([embeddings[word]])[0]
phrases = np.array([w for w in embeddings])
X = np.array([embeddings[w] for w in embeddings])
y = kmeans.predict(X)
cluster_words = phrases[y == cluster]
return cluster, cluster_words
def display_cluster(kmeans, phrase):
cluster, cluster_words = get_kmeans_cluster(kmeans, phrase=phrase)
# print all phrases within the cluster
print(f"Full KMeans ({phrase}, cluster {cluster})")
for i, w in enumerate(cluster_words):
print(i+1, w)
# rank all clusters (excluding this one) by Euclidean distance of their facilities from this cluster's heart
distances = np.concatenate([kmeans.cluster_centers_[:cluster], kmeans.cluster_centers_[cluster+1:]], axis=0)
distances = np.sum(np.sq.(distances - kmeans.cluster_centers_[cluster]), axis=1)
nearest = np.argmin(distances, axis=0)
_, nearest_words = get_kmeans_cluster(kmeans, cluster=nearest)
print(f"Nearest cluster: {nearest}")
for i, w in enumerate(nearest_words[:5]):
print(i+1, w)
farthest = np.argmax(distances, axis=0)
print(f"Farthest cluster: {farthest}")
_, farthest_words = get_kmeans_cluster(kmeans, cluster=farthest)
for i, w in enumerate(farthest_words[:5]):
print(i+1, w)

Now let’s check out this code.

display_cluster(kmeans, 'animal')
# species, fish, wild, canine, bear, males, birds...
display_cluster(kmeans, 'canine')
# similar as 'animal'
display_cluster(kmeans, 'birds')
# similar once more
display_cluster(kmeans, 'chook')
# unfold, chook, flu, virus, examined, people, outbreak, contaminated, sars....?

You won’t get precisely this outcome each time: the clustering algorithm is non-deterministic. However a lot of the time, “birds” is related to illness phrases fairly than animal phrases. It appears the unique dataset tends to make use of the phrase “chook” within the context of illness vectors.

There are actually tons of extra clusters so that you can discover the contents of. Another clusters I discovered attention-grabbing are “Illinois” and “Genghis”.

Principal Part Evaluation (PCA) is a software we are able to use to search out the instructions in vector area related to probably the most variance in our dataset. Let’s attempt it. Like clustering, sklearn makes this simple.

from sklearn.decomposition import PCA
def get_pca_vecs(n=10): # get the primary 10 principal elements
pca = PCA()
X = np.array([embeddings[w] for w in embeddings])
pca.match(X)
principal_components = listing(pca.components_[:n, :])
return pca, principal_components
pca, pca_vecs = get_pca_vecs()
for i, vec in enumerate(pca_vecs):
# show the phrases with the best and lowest values for every principal element
display_sims(to_e=vec, metric=cos_sim, label=f'PCA {i+1}')
display_sims(to_e=vec, metric=cos_sim, label=f'PCA {i+1} unfavourable', reverse=True)

Like our ok-means experiment, lots of these PCA vectors are actually attention-grabbing. For instance, let’s check out principal element 9:

    PCA 9
1 that includes: 0.38193
2 hindi: 0.37217
3 arabic: 0.36029
4 sung: 0.35130
5 che: 0.34819
6 malaysian: 0.34474
7 ka: 0.33820
8 video: 0.33549
9 bollywood: 0.33347
10 counterpart: 0.33343
PCA 9 unfavourable
1 suffolk: -0.31999
2 cumberland: -0.31697
3 northumberland: -0.31449
4 hampshire: -0.30857
5 missouri: -0.30771
6 calhoun: -0.30749
7 erie: -0.30345
8 massachusetts: -0.30133
9 counties: -0.29710
10 wyoming: -0.29613

It appears like constructive values for element 9 are related to Center Jap, South Asian and Southeast Asian phrases, whereas unfavourable values are related to North American and British phrases.

One other attention-grabbing one is element 3. All of the constructive phrases are decimal numbers, apparently fairly a salient function for this mannequin. Part 8 additionally reveals an identical sample.

    PCA 3
1 1.8: 0.57993
2 1.6: 0.57851
3 1.2: 0.57841
4 1.4: 0.57294
5 2.3: 0.57019
6 2.6: 0.56993
7 2.8: 0.56966
8 3.7: 0.56660
9 1.9: 0.56424
10 2.2: 0.56063

Dimensionality Discount

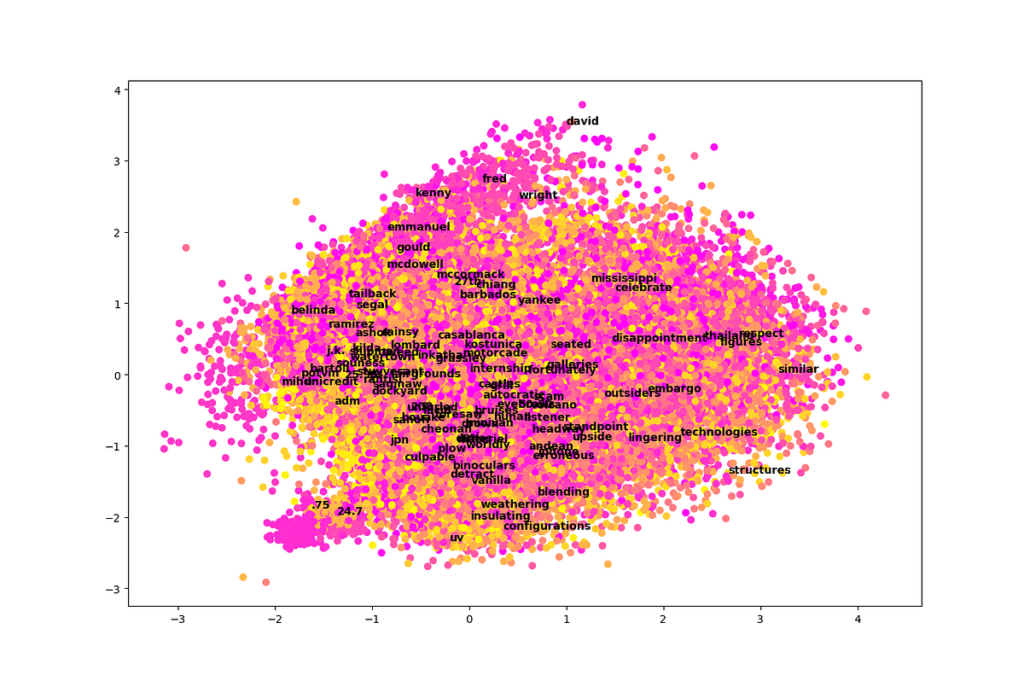
One of many essential advantages of PCA is that it permits us to take a really high-dimensional dataset (300-dimensional on this case) and plot it in simply two or three dimensions by projecting onto the primary elements. Let’s attempt a two-dimensional plot and see if there may be any info we are able to collect from it. We’ll additionally embody color-coding by cluster utilizing ok-means.

def plot_pca(pca_vecs, kmeans):
phrases = [w for w in embeddings]
x_vec = pca_vecs[0]
y_vec = pca_vecs[1]
X = np.array([np.dot(x_vec, embeddings[w]) for w in phrases])
Y = np.array([np.dot(y_vec, embeddings[w]) for w in phrases])
colours =  kmeans.predict([embeddings[w] for w in phrases])
plt.scatter(X, Y, c=colours, cmap='spring') # shade by cluster
for i in np.random.alternative(len(phrases), dimension=100, exchange=False):
# annotate 100 randomly chosen phrases on the graph
plt.annotate(phrases[i], (X[i], Y[i]), weight='daring')
plt.present()
plot_pca(pca_vecs, kmeans)

Sadly, this plot is a complete mess! It’s troublesome to be taught a lot from it. It appears like simply two dimensions in isolation are usually not very simple to interpret amongst 300 whole dimensions, at the very least within the case of this dataset.

There are two exceptions. First, we see that names are inclined to cluster close to the highest of this graph. Second, there’s a little part that stands out like a sore thumb on the backside left. This space seems to be related to numbers, significantly decimal numbers.

It’s usually useful to get an concept of the covariance between enter options. On this case, our enter options are simply summary vector instructions which might be troublesome to interpret. Nonetheless, a covariance matrix can inform us how a lot of this info is definitely getting used. If we see excessive covariance, it means some dimensions are strongly correlated, and possibly we might get away with lowering the dimensionality slightly bit.

def display_covariance():
X = np.array([embeddings[w] for w in embeddings]).T # rows are variables (elements), columns are observations (phrases)
cov = np.cov(X)
cov_range = np.most(np.max(cov), np.abs(np.min(cov))) # be sure that the colorbar is balanced, with 0 within the center
plt.imshow(cov, cmap='bwr', interpolation='nearest', vmin=-cov_range, vmax=cov_range)
plt.colorbar()
plt.present()
display_covariance()

After all, there’s a giant line down the main diagonal, representing that every element is strongly correlated with itself. Apart from that, this isn’t a really attention-grabbing graph. Every part appears largely clean, which is an efficient signal.

When you look intently, there’s one exception: elements 9 and 276 appear considerably strongly associated (covariance of 0.308).

Let’s examine this additional by printing the vectors which might be most related to elements 9 and 276. That is equal to cosine similarity to a foundation vector of all zeros, aside from a one within the related element.

e9 = np.zeros_like(zero_vec)
e9[9] = 1.0
e276 = np.zeros_like(zero_vec)
e276[276] = 1.0
display_sims(to_e=e9, metric=cos_sim, label='e9')
# grizzlies, supersonics, notables, posey, bobcats, wannabe, hoosiers...
display_sims(to_e=e276, metric=cos_sim, label='e276')
# pehr, zetsche, steadied, 202-887-8307, bernice, goldie, edelman, kr...

These outcomes are unusual, and never very informative.

However wait: we are able to even have a constructive covariance in these elements if phrases with a really unfavourable worth in a single are inclined to even be very unfavourable within the different. Let’s attempt reversing the course of similarity.

display_sims(to_e=e9, metric=cos_sim, label='e9', reverse=True)
# due to this fact, that, it, which, authorities, as a result of, furthermore, reality, thus, very
display_sims(to_e=e276, metric=cos_sim, label='e276', reverse=True)
# they, as an alternative, these, tons of, addition, dozens, others, dozen, solely, exterior

It appears like each of those elements are related to primary operate phrases and numbers that may be present in many various contexts. This helps clarify the covariance between them, at the very least extra so than the constructive case did.

On this article we utilized a wide range of exploratory information evaluation (EDA) strategies to a 300-dimensional dataset of GloVe phrase embeddings. We used cosine similarity to measure the similarity between the which means of phrases, clustering to group phrases into associated teams, and principal element evaluation (PCA) to establish the instructions in vector area which might be most necessary to the embedding mannequin.

We visually noticed total minimal covariance between the enter options utilizing principal element evaluation. We tried utilizing PCA to plot all of our 300-dimensional information in simply two dimensions, however this was nonetheless slightly messy.

We additionally examined assumptions and biases in our dataset. We recognized gender bias in our dataset by evaluating the cosine similarity of nurse with every of man and girl. We tried utilizing vector math to signify analogies (like “king” is to “queen” as “man” is to “girl”), with some success. By subtracting numerous examples of vectors referring to men and women, we have been capable of uncover a vector course related to gender, and show the “most masculine” and “most female” vectors within the dataset.

There’s much more EDA you could possibly attempt on a dataset of phrase embeddings, however I hope this was an excellent place to begin to know each some strategies of EDA usually and the construction of phrase embeddings specifically. If you wish to see the complete code related to this text, plus some further examples, you possibly can take a look at my GitHub at crackalamoo/glove-embeddings-eda. Thanks for studying!

References

[1] J. Pennington, R. Socher and C.Manning, GloVe: Global Vectors for Word Representation (2014), Stanford NLP (Public Area Dataset)

[2] T. Bolukbasi, Okay. Chang, J. Zou, V. Saligrama and A. Kalai, Man is to Computer Programmer as Woman is to Homemaker? Debiasing Word Embeddings (2016), Microsoft Analysis New England

All photos created by the writer utilizing Matplotlib.