We then preprocess the information by merging the 2 tables, scaling the numerical options, and OneHotEncoding the explicit options. We will then arrange an LSTM mannequin that processes the sequences of touchpoints after embedding them. Within the ultimate totally linked layer, we additionally add the contextual options of the shopper. The total code for preprocessing and coaching could be discovered on this notebook.
We will then prepare the neural community with a binary cross-entropy loss. I’ve plotted the recall achieved on the check set under. On this case, we care extra about recall than accuracy as we wish to detect as many changing prospects as attainable. Wrongly predicting that some prospects will convert in the event that they don’t isn’t as dangerous as lacking high-potential prospects.
Moreover, we are going to discover that the majority journeys don’t result in a conversion. We’ll usually see conversion charges from 2% to 7% which implies that we’ve a extremely imbalanced dataset. For a similar purpose, accuracy isn’t all that significant. All the time predicting the bulk class (on this case ‘no conversion’) will get us a really excessive accuracy however we gained’t discover any of the changing customers.
As soon as we’ve a skilled mannequin, we are able to use it to design optimum journeys. We will impose a sequence of channels (within the instance under channel 1 then 2) on a set of consumers and take a look at the conversion chance predicted by the mannequin. We will already see that these fluctuate quite a bit relying on the traits of the shopper. Due to this fact, we wish to optimize the journey for every buyer individually.
Moreover, we are able to’t simply choose the highest-probability sequence. Actual-world advertising has constraints:
- Channel-specific limitations (e.g., e mail frequency caps)
- Required touchpoints at particular positions
- Finances constraints
- Timing necessities
Due to this fact, we body this as a constrained combinatorial optimization downside: discover the sequence of touchpoints that maximizes the mannequin’s predicted conversion chance whereas satisfying all constraints. On this case, we are going to solely constrain the incidence of touchpoints at sure locations within the journey. That’s, we’ve a mapping from place to touchpoint that specifies {that a} sure touchpoint should happen at a given place.
Word additionally that we goal to optimize for a predefined journey size fairly than journeys of arbitrary size. By the character of the simulation, the general conversion chance shall be strictly monotonically rising as we’ve a non-zero conversion chance at every touchpoint. Due to this fact, an extended journey (extra non-zero entries) would trump a shorter journey more often than not and we’d assemble infinitely lengthy journeys.
Optimization utilizing Beam Search
Beneath is the implementation for beam search utilizing recursion. At every degree, we optimize a sure place within the journey. If the place is within the constraints and already mounted, we skip it. If we’ve reached the utmost size we wish to optimize, we cease recursing and return.
At every degree, we take a look at present options and generate candidates. At any level, we hold the perfect Ok candidates outlined by the beam width. These finest candidates are then used as enter for the subsequent spherical of beam search the place we optimize the subsequent place within the sequence.
def beam_search_step(
mannequin: JourneyLSTM,
X: torch.Tensor,
pos: int,
num_channels: int,
max_length: int,
constraints:dict[int, int],
beam_width: int = 3
):
if pos > max_length:
return Xif pos in constraints:
return beam_search_step(mannequin, X, pos + 1, num_channels, max_length, constraints, beam_width)
candidates = [] # Checklist to retailer (sequence, rating) tuples
for sequence_idx in vary(min(beam_width, len(X))):
X_current = X[sequence_idx:sequence_idx+1].clone()
# Attempt every attainable channel
for channel in vary(num_channels):
X_candidate = X_current.clone()
X_candidate[0, extra_dim + pos] = channel
# Get prediction rating
pred = mannequin(X_candidate)[0].merchandise()
candidates.append((X_candidate, pred))
candidates.kind(key=lambda x: x[1], reverse=True)
best_candidates = candidates[:beam_width]
X_next = torch.cat([cand[0] for cand in best_candidates], dim=0)
# Recurse with finest candidates
return beam_search_step(mannequin, X_next, pos + 1, num_channels, max_length, constraints, beam_width)
This optimization strategy is grasping and we’re prone to miss high-probability mixtures. Nonetheless, in lots of eventualities, particularly with many channels, brute forcing an optimum answer might not be possible because the variety of attainable journeys grows exponentially with the journey size.
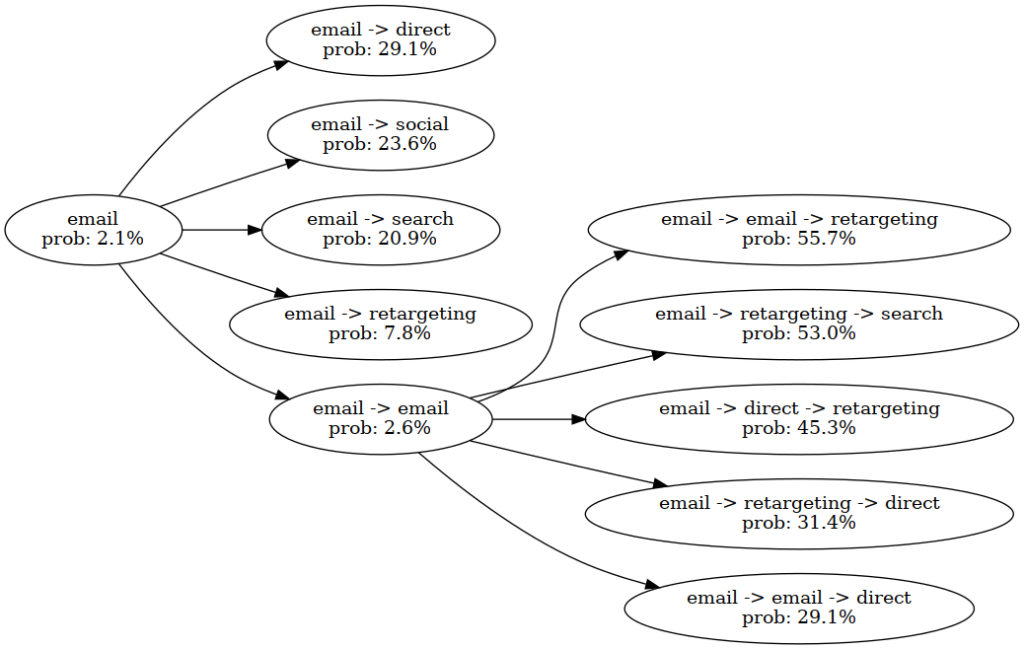
Within the picture above, we optimized the conversion chance for a single buyer. In place 0, we’ve specified ‘e mail’ as a set touchpoint. Then, we discover attainable mixtures with e mail. Since we’ve a beam width of 5, all mixtures (e.g. e mail -> search) go into the subsequent spherical. In that spherical, we found the high-potential journey which might show the consumer two instances e mail and eventually retarget.
Shifting from prediction to optimization in attribution modeling means we’re going from predictive to prescriptive modeling the place the mannequin tells us actions to take. This has the potential to realize a lot larger conversion charges, particularly when we’ve extremely complicated eventualities with many channels and contextual variables.
On the identical time, this strategy has a number of drawbacks. Firstly, if we wouldn’t have a mannequin that may detect changing prospects sufficiently effectively, we’re prone to hurt conversion charges. Moreover, the possibilities that the mannequin outputs need to be calibrated effectively. Otherwiese, the conversion possibilities we’re optimizing for are possible not meanningful. Lastly, we are going to encounter issues when the mannequin has to foretell journeys which can be outdoors of its information distribution. It will due to this fact even be fascinating to make use of a Reinforcement Studying (RL) strategy, the place the mannequin can actively generate new coaching information.