In statistics, a standard level of confusion for a lot of learners is why we divide by n−1 when calculating pattern variance, fairly than merely utilizing n, the variety of observations within the pattern. This alternative could seem small however is a important adjustment that corrects for a pure bias that happens after we estimate the variance of a inhabitants from a pattern. Let’s stroll via the reasoning in easy language, with examples to grasp why dividing by n−1, generally known as Bessel’s correction, is critical.
The core idea of correction (in Bessel’s correction), is that we are inclined to appropriate our estimation, however a transparent query is estimation of what? So by making use of Bessel’s correction we are inclined to appropriate the estimation of deviations calculated from our assumed pattern imply, our assumed pattern imply will not often ever co-inside with the precise inhabitants imply, so it’s protected to imagine that in 99.99% (much more than that in actual) instances our pattern imply wouldn’t be equal to the inhabitants imply. We do all of the calculations based mostly on this assumed pattern imply, that’s we estimate the inhabitants parameters via the imply of this pattern.
Studying additional down the weblog, one would get a transparent instinct that why in all of these 99.99% instances (in all of the instances besides leaving the one, by which pattern imply = inhabitants imply), we are inclined to underestimate the deviations from precise deviations, so to compensate this underestimation error, diving by a smaller quantity than ’n’ do the job, so diving by n-1 as an alternative of n, accounts for the compensation of the underestimation that’s achieved in calculating the deviations from the pattern imply.
Begin studying down from right here and also you’ll ultimately perceive…
When we’ve got a whole inhabitants of knowledge factors, the variance is calculated by discovering the imply (common), then figuring out how every level deviates from this imply, squaring these deviations, summing them up, and at last dividing by n, the entire variety of factors within the inhabitants. This provides us the inhabitants variance.
Nonetheless, if we don’t have knowledge for a whole inhabitants and are as an alternative working with only a pattern, we estimate the inhabitants variance. However right here lies the issue: when utilizing solely a pattern, we don’t know the true inhabitants imply (denoted as μ), so we use the pattern imply (x_bar) as an alternative.
To grasp why we divide by n−1 within the case of samples, we have to look carefully at what occurs after we use the pattern imply fairly than the inhabitants imply. For real-life functions, counting on pattern statistics is the one choice we’ve got. Right here’s the way it works:
Once we calculate variance in a pattern, we discover every knowledge level’s deviation from the pattern imply, sq. these deviations, after which take the common of those squared deviations. Nonetheless, the pattern imply is often not precisely equal to the inhabitants imply. Because of this distinction, utilizing the pattern imply tends to underestimate the true unfold or variance within the inhabitants.
Let’s break it down with all potential instances that may occur (three completely different instances), I’ll give an in depth walkthrough on the primary case, identical precept applies to the opposite two instances as effectively, detailed walkthrough has been given for case 1.
1. When the Pattern Imply is Much less Than the Inhabitants Imply (x_bar < inhabitants imply)
If our pattern imply (x_bar) is lower than the inhabitants imply (μ), then most of the factors within the pattern can be nearer to (x_bar) than they might be to μ. Because of this, the distances (deviations) from the imply are smaller on common, resulting in a smaller variance calculation. This implies we’re underestimating the precise variance.
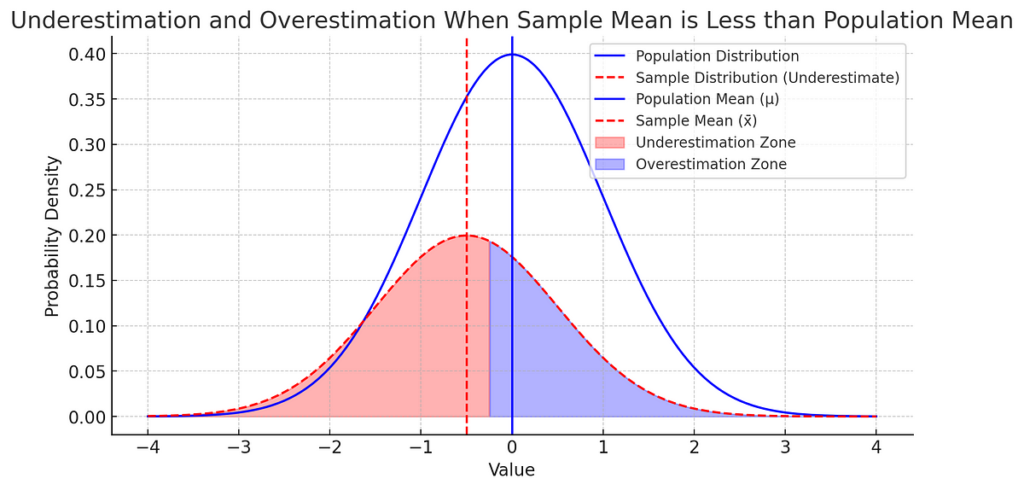
Clarification of the graph given under — The smaller regular distribution is of our pattern and the larger regular distribution is of our inhabitants (within the above case the place x_bar < inhabitants imply), the plot would appear like the one proven under.
As we’ve got knowledge factors of our pattern, as a result of that’s what we will accumulate, can’t accumulate all the info factors of the inhabitants as a result of that’s merely not potential. For all the info factors in our pattern on this case, from damaging infinity, to the mid level of x_bar and inhabitants imply, absolutely the or squared distinction (deviations) between the pattern factors and inhabitants imply could be larger than absolutely the or squared distinction (deviations) between pattern factors and pattern imply and on the correct aspect of the midpoint until optimistic infinity, the deviations calculated with respect to pattern imply could be larger than the deviations calculated utilizing inhabitants imply. The area is indicated within the graph under for the above case, because of the symmetric nature of the conventional curve we will absolutely say that the underestimation zone could be bigger than the overestimation zone which can also be highlighted within the graph under, which ends up in an general underestimation of the deviations.
So to compensate the underestimation, we divide the deviations by a quantity smaller than pattern dimension ’n’, which is ‘n-1’ which is named Bessel’s correction.
2. When the Pattern Imply is Better Than the Inhabitants Imply
If the pattern imply is bigger than the inhabitants imply, we’ve got the reverse scenario: knowledge factors on the low finish of the pattern can be nearer to x_bar than to μ, nonetheless leading to an underestimation of variance.
Based mostly on the small print laid above, it’s clear that on this case additionally underestimation zone is bigger than the overestimation zone, so on this case additionally we’ll account for this underestimation by dividing the deviations by ‘n-1’ as an alternative of n.
3. When the Pattern Imply is Precisely Equal to the Inhabitants Imply (0.000001%)
This case is uncommon, and provided that the pattern imply is completely aligned with the inhabitants imply would our estimate be unbiased. Nonetheless, this alignment virtually by no means occurs by probability, so we typically assume that we’re underestimating.
Clearly, deviations calculated for the pattern factors with respect to pattern imply are precisely the identical because the deviations calculated with respect to the inhabitants imply, as a result of the pattern imply and inhabitants imply each are equal. This may yield no underestimation or overestimation zone.
Briefly, any distinction between x_bar and μ (which nearly all the time happens) leads us to underestimate the variance. This is the reason we have to make a correction by dividing by n−1, which accounts for this bias.
Dividing by n−1 is known as Bessel’s correction and compensates for the pure underestimation bias in pattern variance. Once we divide by n−1, we’re successfully making a small adjustment that spreads out our variance estimate, making it a greater reflection of the true inhabitants variance.
One can relate all this to levels of freedom too , some information of dofs are required to grasp from the perspective of levels of freedom-
In a pattern, one diploma of freedom is “used up” by calculating the pattern imply. This leaves us with n−1 unbiased knowledge factors that contribute details about the variance, which is why we divide by n−1 fairly than n.
If our pattern dimension could be very small, the distinction between dividing by n and n−1 turns into extra vital. As an illustration, in case you have a pattern dimension of 10:
- Dividing by n would imply dividing by 10, which can vastly underestimate the variance.
- Dividing by n−1 or 9, supplies a greater estimate, compensating for the small pattern.
But when your pattern dimension is giant (say, 10,000), the distinction between dividing by 10,000 or 9,999 is tiny, so the influence of Bessel’s correction is minimal.
If we don’t use Bessel’s correction, our pattern variance will typically underestimate the inhabitants variance. This could have cascading results, particularly in statistical modelling and speculation testing, the place correct variance estimates are essential for drawing dependable conclusions.
As an illustration:
- Confidence intervals: Variance estimates affect the width of confidence intervals round a pattern imply. Underestimating variance might result in narrower intervals, giving a misunderstanding of precision.
- Speculation exams: Many statistical exams, such because the t-test, depend on correct variance estimates to find out if noticed results are vital. Underestimating variance might make it more durable to detect true variations.
The selection to divide by n−1 isn’t arbitrary. Whereas we received’t go into the detailed proof right here, it’s grounded in mathematical concept. Dividing by n−1 supplies an unbiased estimate of the inhabitants variance when calculated from a pattern. Different changes, comparable to n−2, would overcorrect and result in an overestimation of variance.
Think about you will have a small inhabitants with a imply weight of 70 kg. Now let’s say you are taking a pattern of 5 individuals from this inhabitants, and their weights (in kg) are 68, 69, 70, 71, and 72. The pattern imply is precisely 70 kg — equivalent to the inhabitants imply by coincidence.
Now suppose we calculate the variance:
- With out Bessel’s correction: we’d divide the sum of squared deviations by n=5.
- With Bessel’s correction: we divide by n−1=4.
Utilizing Bessel’s correction on this method barely will increase our estimate of the variance, making it nearer to what the inhabitants variance could be if we calculated it from the entire inhabitants as an alternative of only a pattern.
Dividing by n−1 when calculating pattern variance might look like a small change, however it’s important to attain an unbiased estimate of the inhabitants variance. This adjustment, generally known as Bessel’s correction, accounts for the underestimation that happens because of counting on the pattern imply as an alternative of the true inhabitants imply.
In abstract:
- Utilizing n−1 compensates for the truth that we’re basing variance on a pattern imply, which tends to underestimate true variability.
- The correction is particularly essential with small pattern sizes, the place dividing by n would considerably distort the variance estimate.
- This follow is prime in statistics, affecting all the things from confidence intervals to speculation exams, and is a cornerstone of dependable knowledge evaluation.
By understanding and making use of Bessel’s correction, we make sure that our statistical analyses replicate the true nature of the info we research, resulting in extra correct and reliable conclusions.