Be aware: Take a look at my earlier article for a sensible dialogue on why Bayesian modeling could be the proper selection to your activity.
This tutorial will deal with a workflow + code walkthrough for constructing a Bayesian regression mannequin in STAN, a probabilistic programming language. STAN is broadly adopted and interfaces along with your language of selection (R, Python, shell, MATLAB, Julia, Stata). See the installation information and documentation.
I’ll use Pystan for this tutorial, just because I code in Python. Even in case you use one other language, the overall Bayesian practices and STAN language syntax I’ll talk about right here doesn’t differ a lot.
For the extra hands-on reader, here’s a hyperlink to the notebook for this tutorial, a part of my Bayesian modeling workshop at Northwestern College (April, 2024).
Let’s dive in!
Lets discover ways to construct a easy linear regression mannequin, the bread and butter of any statistician, the Bayesian approach. Assuming a dependent variable Y and covariate X, I suggest the next easy model-
Y = α + β * X + ϵ
The place ⍺ is the intercept, β is the slope, and ϵ is a few random error. Assuming that,
ϵ ~ Regular(0, σ)
we will present that
Y ~ Regular(α + β * X, σ)
We’ll discover ways to code this mannequin type in STAN.
Generate Information
First, let’s generate some pretend knowledge.
#Mannequin Parameters
alpha = 4.0 #intercept
beta = 0.5 #slope
sigma = 1.0 #error-scale
#Generate pretend knowledge
x = 8 * np.random.rand(100)
y = alpha + beta * x
y = np.random.regular(y, scale=sigma) #noise
#visualize generated knowledge
plt.scatter(x, y, alpha = 0.8)
Now that we now have some knowledge to mannequin, let’s dive into how one can construction it and move it to STAN together with modeling directions. That is executed through the mannequin string, which generally incorporates 4 (often extra) blocks- knowledge, parameters, mannequin, and generated portions. Let’s talk about every of those blocks intimately.
DATA block
knowledge { //enter the info to STAN
int<decrease=0> N;
vector[N] x;
vector[N] y;
}
The knowledge block is probably the only, it tells STAN internally what knowledge it ought to anticipate, and in what format. As an example, right here we pass-
N: the scale of our dataset as kind int. The <decrease=0> half declares that N≥0. (Although it’s apparent right here that knowledge size can’t be damaging, stating these bounds is nice commonplace apply that may make STAN’s job simpler.)
x: the covariate as a vector of size N.
y: the dependent as a vector of size N.
See docs here for a full vary of supported knowledge sorts. STAN provides help for a variety of sorts like arrays, vectors, matrices and so forth. As we noticed above, STAN additionally has help for encoding limits on variables. Encoding limits is really helpful! It results in higher specified fashions and simplifies the probabilistic sampling processes working below the hood.
Mannequin Block
Subsequent is the mannequin block, the place we inform STAN the construction of our mannequin.
//easy mannequin block
mannequin {
//priors
alpha ~ regular(0,10);
beta ~ regular(0,1); //mannequin
y ~ regular(alpha + beta * x, sigma);
}
The mannequin block additionally incorporates an necessary, and infrequently complicated, factor: prior specification. Priors are a quintessential a part of Bayesian modeling, and have to be specified suitably for the sampling activity.
See my earlier article for a primer on the function and instinct behind priors. To summarize, the prior is a presupposed practical type for the distribution of parameter values — usually referred to, merely, as prior perception. Although priors don’t have to precisely match the ultimate answer, they have to enable us to pattern from it.
In our instance, we use Regular priors of imply 0 with completely different variances, relying on how positive we’re of the equipped imply worth: 10 for alpha (very uncertain), 1 for beta (considerably positive). Right here, I equipped the overall perception that whereas alpha can take a variety of various values, the slope is mostly extra contrained and received’t have a big magnitude.
Therefore, within the instance above, the prior for alpha is ‘weaker’ than beta.
As fashions get extra difficult, the sampling answer area expands, and supplying beliefs positive aspects significance. In any other case, if there is no such thing as a robust instinct, it’s good apply to only provide much less perception into the mannequin i.e. use a weakly informative prior, and stay versatile to incoming knowledge.
The shape for y, which you might need acknowledged already, is the usual linear regression equation.
Generated Portions
Lastly, we now have our block for generated portions. Right here we inform STAN what portions we need to calculate and obtain as output.
generated portions { //get portions of curiosity from fitted mannequin
vector[N] yhat;
vector[N] log_lik;
for (n in 1:N) alpha + x[n] * beta, sigma);
//chance of knowledge given the mannequin and parameters
}
Be aware: STAN helps vectors to be handed both straight into equations, or as iterations 1:N for every factor n. In apply, I’ve discovered this help to vary with completely different variations of STAN, so it’s good to attempt the iterative declaration if the vectorized model fails to compile.
Within the above example-
yhat: generates samples for y from the fitted parameter values.
log_lik: generates chance of knowledge given the mannequin and fitted parameter worth.
The aim of those values shall be clearer after we discuss mannequin analysis.
Altogether, we now have now absolutely specified our first easy Bayesian regression mannequin:
mannequin = """
knowledge { //enter the info to STAN
int<decrease=0> N;
vector[N] x;
vector[N] y;
}
parameters {
actual alpha;
actual beta;
actual<decrease=0> sigma;
}mannequin {
alpha ~ regular(0,10);
beta ~ regular(0,1);
y ~ regular(alpha + beta * x, sigma);
}generated portions {
vector[N] yhat;
vector[N] log_lik;for (n in 1:N) alpha + x[n] * beta, sigma);
}
"""
All that continues to be is to compile the mannequin and run the sampling.
#STAN takes knowledge as a dict
knowledge = {'N': len(x), 'x': x, 'y': y}
STAN takes enter knowledge within the type of a dictionary. It is vital that this dict incorporates all of the variables that we advised STAN to anticipate within the model-data block, in any other case the mannequin received’t compile.
#parameters for STAN becoming
chains = 2
samples = 1000
warmup = 10
# set seed
# Compile the mannequin
posterior = stan.construct(mannequin, knowledge=knowledge, random_seed = 42)
# Practice the mannequin and generate samples
match = posterior.pattern(num_chains=chains, num_samples=samples)The .pattern() technique parameters management the Hamiltonian Monte Carlo (HMC) sampling course of, the place —
- num_chains: is the variety of occasions we repeat the sampling course of.
- num_samples: is the variety of samples to be drawn in every chain.
- warmup: is the variety of preliminary samples that we discard (because it takes a while to achieve the overall neighborhood of the answer area).
Understanding the appropriate values for these parameters depends upon each the complexity of our mannequin and the sources accessible.
Greater sampling sizes are in fact ideally suited, but for an ill-specified mannequin they may show to be simply waste of time and computation. Anecdotally, I’ve had massive knowledge fashions I’ve needed to wait every week to complete operating, solely to search out that the mannequin didn’t converge. Is is necessary to begin slowly and sanity examine your mannequin earlier than operating a full-fledged sampling.
Mannequin Analysis
The generated portions are used for
- evaluating the goodness of match i.e. convergence,
- predictions
- mannequin comparability
Convergence
Step one for evaluating the mannequin, within the Bayesian framework, is visible. We observe the sampling attracts of the Hamiltonian Monte Carlo (HMC) sampling course of.
In simplistic phrases, STAN iteratively attracts samples for our parameter values and evaluates them (HMC does approach extra, however that’s past our present scope). For a superb match, the pattern attracts should converge to some frequent common space which might, ideally, be the worldwide optima.
The determine above exhibits the sampling attracts for our mannequin throughout 2 unbiased chains (pink and blue).
- On the left, we plot the general distribution of the fitted parameter worth i.e. the posteriors. We anticipate a regular distribution if the mannequin, and its parameters, are properly specified. (Why is that? Properly, a traditional distribution simply implies that there exist a sure vary of greatest match values for the parameter, which speaks in help of our chosen mannequin type). Moreover, we must always anticipate a substantial overlap throughout chains IF the mannequin is converging to an optima.
- On the appropriate, we plot the precise samples drawn in every iteration (simply to be further positive). Right here, once more, we want to see not solely a slender vary but in addition quite a lot of overlap between the attracts.
Not all analysis metrics are visible. Gelman et al. [1] additionally suggest the Rhat diagnostic which important is a mathematical measure of the pattern similarity throughout chains. Utilizing Rhat, one can outline a cutoff level past which the 2 chains are judged too dissimilar to be converging. The cutoff, nonetheless, is tough to outline because of the iterative nature of the method, and the variable warmup intervals.
Visible comparability is therefore a vital part, no matter diagnostic exams
A frequentist thought you will have right here is that, “properly, if all we now have is chains and distributions, what’s the precise parameter worth?” That is precisely the purpose. The Bayesian formulation solely offers in distributions, NOT level estimates with their hard-to-interpret check statistics.
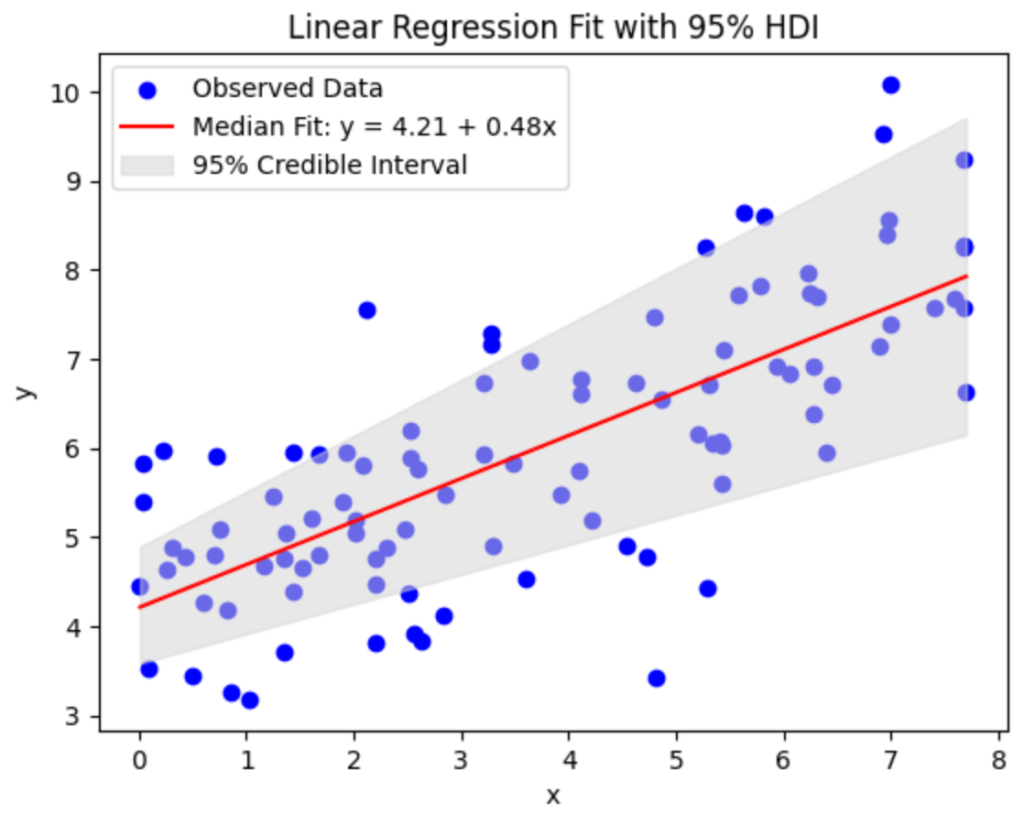
That stated, the posterior can nonetheless be summarized utilizing credible intervals just like the Excessive Density Interval (HDI), which incorporates all of the x% highest chance density factors.
It is very important distinction Bayesian credible intervals with frequentist confidence intervals.
- The credible interval provides a chance distribution on the doable values for the parameter i.e. the chance of the parameter assuming every worth in some interval, given the info.
- The arrogance interval regards the parameter worth as fastened, and estimates as a substitute the arrogance that repeated random samplings of the info would match.
Therefore the
Bayesian method lets the parameter values be fluid and takes the info at face worth, whereas the frequentist method calls for that there exists the one true parameter worth… if solely we had entry to all the info ever
Phew. Let that sink in, learn it once more till it does.
One other necessary implication of utilizing credible intervals, or in different phrases, permitting the parameter to be variable, is that the predictions we make seize this uncertainty with transparency, with a sure HDI % informing the perfect match line.
Mannequin comparability
Within the Bayesian framework, the Watanabe-Akaike Data Metric (WAIC) rating is the broadly accepted selection for mannequin comparability. A easy clarification of the WAIC rating is that it estimates the mannequin chance whereas regularizing for the variety of mannequin parameters. In easy phrases, it may possibly account for overfitting. That is additionally main draw of the Bayesian framework — one does not essentially want to hold-out a mannequin validation dataset. Therefore,
Bayesian modeling provides a vital benefit when knowledge is scarce.
The WAIC rating is a comparative measure i.e. it solely holds that means when put next throughout completely different fashions that try to elucidate the identical underlying knowledge. Thus in apply, one can preserve including extra complexity to the mannequin so long as the WAIC will increase. If sooner or later on this strategy of including maniacal complexity, the WAIC begins dropping, one can name it a day — any extra complexity won’t supply an informational benefit in describing the underlying knowledge distribution.
Conclusion
To summarize, the STAN mannequin block is solely a string. It explains to STAN what you’ll give to it (mannequin), what’s to be discovered (parameters), what you assume is occurring (mannequin), and what it ought to offer you again (generated portions).
When turned on, STAN easy turns the crank and offers its output.
The true problem lies in defining a correct mannequin (refer priors), structuring the info appropriately, asking STAN precisely what you want from it, and evaluating the sanity of its output.
As soon as we now have this half down, we will delve into the actual energy of STAN, the place specifying more and more difficult fashions turns into only a easy syntactical activity. The truth is, in our subsequent tutorial we’ll do precisely this. We’ll construct upon this easy regression instance to discover Bayesian Hierarchical fashions: an business commonplace, state-of-the-art, defacto… you identify it. We’ll see how one can add group-level radom or fastened results into our fashions, and marvel on the ease of including complexity whereas sustaining comparability within the Bayesian framework.
Subscribe if this text helped, and to stay-tuned for extra!
References
[1] Andrew Gelman, John B. Carlin, Hal S. Stern, David B. Dunson, Aki Vehtari and Donald B. Rubin (2013). Bayesian Information Evaluation, Third Version. Chapman and Corridor/CRC.