Investigating Geoffrey Hinton’s Nobel Prize-winning work and constructing it from scratch utilizing PyTorch
One recipient of the 2024 Nobel Prize in Physics was Geoffrey Hinton for his contributions within the subject of AI and machine studying. Lots of people know he labored on neural networks and is termed the “Godfather of AI”, however few perceive his works. Specifically, he pioneered Restricted Boltzmann Machines (RBMs) many years in the past.
This text goes to be a walkthrough of RBMs and can hopefully present some instinct behind these advanced mathematical machines. I’ll present some code on implementing RBMs from scratch in PyTorch after going by means of the derivations.
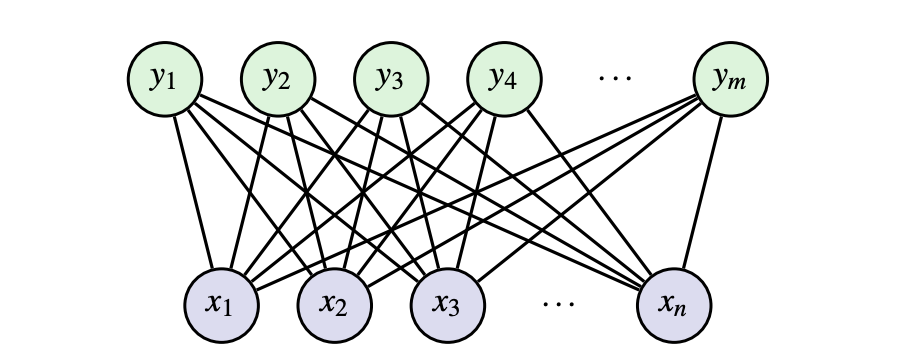
RBMs are a type of unsupervised studying (solely the inputs are used to learn- no output labels are used). This implies we are able to routinely extract significant options within the knowledge with out counting on outputs. An RBM is a community with two several types of neurons with binary inputs: seen, x, and hidden, h. Seen neurons take within the enter knowledge and hidden neurons study to detect options/patterns.
In additional technical phrases, we are saying an RBM is an undirected bipartite graphical mannequin with stochastic binary seen and hidden variables. The primary objective of an RBM is to reduce the power of the joint configuration E(x,h) typically utilizing contrastive studying (mentioned in a while).
An power perform doesn’t correspond to bodily power, nevertheless it does come from physics/statistics. Consider it like a scoring perform. An power perform E assigns decrease scores (energies) to configurations x that we would like our mannequin to choose, and better scores to configurations we would like it to keep away from. The power perform is one thing we get to decide on as mannequin designers.
For RBMs, the power perform is as follows (modeled after the Boltzmann distribution):
The power perform consists of three phrases. The primary one is the interplay between the hidden and visual layer with weights, W. The second is the sum of the bias phrases for the seen items. The third is the sum of the bias phrases for the hidden items.
With the power perform, we are able to calculate the likelihood of the joint configuration given by the Boltzmann distribution. With this likelihood perform, we are able to mannequin our items:
Z is the partition perform (often known as the normalization fixed). It’s the sum of e^(-E) over all attainable configurations of seen and hidden items. The massive problem with Z is that it’s usually computationally intractable to calculate precisely as a result of you want to sum over all attainable configurations of v and h. For instance, with binary items, you probably have m seen items and n hidden items, you want to sum over 2^(m+n) configurations. Subsequently, we’d like a technique to keep away from calculating Z.
With these features and distributions outlined, we are able to go over some derivations for inference earlier than speaking about coaching and implementation. We already talked about the lack to calculate Z within the joint likelihood distribution. To get round this, we are able to use Gibbs Sampling. Gibbs Sampling is a Markov Chain Monte Carlo algorithm for sampling from a specified multivariate likelihood distribution when direct sampling from the joint distribution is tough, however sampling from the conditional distribution is extra sensible [2]. Subsequently, we’d like conditional distributions.
The nice half a couple of restricted Boltzmann versus a totally linked Boltzmann is the truth that there aren’t any connections inside layers. This implies given the seen layer, all hidden items are conditionally impartial and vice versa. Let’s have a look at what that simplifies all the way down to beginning with p(x|h):
We are able to see the conditional distribution simplifies all the way down to a sigmoid perform the place j is the jᵗʰ row of W. There’s a way more rigorous calculation I’ve included within the appendix proving the primary line of this derivation. Attain out if ! Let’s now observe the conditional distribution p(h|x):
We are able to see this conditional distribution additionally simplifies all the way down to a sigmoid perform the place okay is the kᵗʰ row of W. Due to the restricted standards within the RBM, the conditional distributions simplify to straightforward computations for Gibbs Sampling throughout inference. As soon as we perceive what precisely the RBM is attempting to study, we’ll implement this in PyTorch.
As with most of deep studying, we are attempting to reduce the damaging log-likelihood (NLL) to coach our mannequin. For the RBM:
Taking the by-product of this yields:
The primary time period on the left-hand aspect of the equation is named optimistic part as a result of it pushes the mannequin to decrease the power of actual knowledge. This time period entails taking the expectation over hidden items h given the precise coaching knowledge x. Constructive part is simple to compute as a result of we’ve the precise coaching knowledge xᵗ and might compute expectations over h because of the conditional independence.
The second time period is named damaging part as a result of it raises the power of configurations the mannequin at present thinks are doubtless. This time period entails taking the expectation over each x and h beneath the mannequin’s present distribution. It’s arduous to compute as a result of we have to pattern from the mannequin’s full joint distribution P(x,h) (doing this requires Markov chains which might be inefficient to do repeatedly in coaching). The opposite various requires computing Z which we already deemed to be unfeasible. To unravel this drawback of calculating damaging part, we use contrastive divergence.
The important thing concept behind contrastive divergence is to make use of truncated Gibbs Sampling to acquire some extent estimate after okay iterations. We are able to exchange the expectation damaging part with this level estimate.
Usually okay = 1, however the greater okay is, the much less biased the estimate of the gradient will likely be. I cannot present the derivation for the completely different partials with respect to the damaging part (for weight/bias updates), however it may be derived by taking the partial by-product of E(x,h) with respect to the variables. There’s a idea of persistent contrastive divergence the place as an alternative of initializing the chain to xᵗ, we initialize the chain to the damaging pattern of the final iteration. Nonetheless, I cannot go into depth on that both as regular contrastive divergence works sufficiently.
Creating an RBM from scratch entails combining all of the ideas we’ve mentioned into one class. Within the __init__ constructor, we initialize the weights, bias time period for the seen layer, bias time period for the hidden layer, and the variety of iterations for contrastive divergence. All we’d like is the scale of the enter knowledge, the scale of the hidden variable, and okay.
We additionally have to outline a Bernoulli distribution to pattern from. The Bernoulli distribution is clamped to stop an exploding gradient throughout coaching. Each of those distributions are used within the ahead cross (contrastive divergence).
class RBM(nn.Module):
"""Restricted Boltzmann Machine template."""def __init__(self, D: int, F: int, okay: int):
"""Creates an occasion RBM module.
Args:
D: Dimension of the enter knowledge.
F: Dimension of the hidden variable.
okay: Variety of MCMC iterations for damaging sampling.
The perform initializes the burden (W) and biases (c & b).
"""
tremendous().__init__()
self.W = nn.Parameter(torch.randn(F, D) * 1e-2) # Initialized from Regular(imply=0.0, variance=1e-4)
self.c = nn.Parameter(torch.zeros(D)) # Initialized as 0.0
self.b = nn.Parameter(torch.zeros(F)) # Initilaized as 0.0
self.okay = okay
def pattern(self, p):
"""Pattern from a bernoulli distribution outlined by a given parameter."""
p = torch.clamp(p, 0, 1)
return torch.bernoulli(p)
The subsequent strategies to construct out the RBM class are the conditional distributions. We derived each of those conditionals earlier:
def P_h_x(self, x):
"""Steady conditional likelihood calculation"""
linear = torch.sigmoid(F.linear(x, self.W, self.b))
return lineardef P_x_h(self, h):
"""Steady seen unit activation"""
return self.c + torch.matmul(h, self.W)
The ultimate strategies entail the implementation of the ahead cross and the free power perform. The power perform represents an efficient power for seen items after summing out all attainable hidden unit configurations. The ahead perform is basic contrastive divergence for Gibbs Sampling. We initialize x_negative, then for okay iterations: acquire h_k from P_h_x and x_negative, pattern h_k from a Bernoulli, acquire x_k from P_x_h and h_k, after which acquire a brand new x_negative.
def free_energy(self, x):
"""Numerically secure free power calculation"""
seen = torch.sum(x * self.c, dim=1)
linear = F.linear(x, self.W, self.b)
hidden = torch.sum(torch.log(1 + torch.exp(linear)), dim=1)
return -visible - hiddendef ahead(self, x):
"""Contrastive divergence ahead cross"""
x_negative = x.clone()
for _ in vary(self.okay):
h_k = self.P_h_x(x_negative)
h_k = self.pattern(h_k)
x_k = self.P_x_h(h_k)
x_negative = self.pattern(x_k)
return x_negative, x_k
Hopefully this supplied a foundation into the speculation behind RBMs in addition to a primary coding implementation class that can be utilized to coach an RBM. With any code or additional derviations, be at liberty to achieve out for extra info!
Derivation for general p(h|x) being the product of every particular person conditional distribution:
[1] Montufar, Guido. “Restricted Boltzmann Machines: Introduction and Assessment.” arXiv:1806.07066v1 (June 2018).
[2] https://en.wikipedia.org/wiki/Gibbs_sampling
[3] Hinton, Geoffrey. “Coaching Merchandise of Consultants by Minimizing Contrastive Divergence.” Neural Computation (2002).