In lots of experiments, not all people assigned to obtain a remedy really take it or use it. For instance, an organization could ship low cost coupons to prospects, intending for them to make use of these coupons to make a purchase order now, which may subsequently enhance their future purchases. Nonetheless, not all prospects will redeem the coupon.
This situation represents “imperfect compliance” (see here), the place remedy task doesn’t all the time result in remedy uptake. To estimate the impression of providing the coupon on future buyer purchases, we should distinguish between two foremost approaches:
- Intention to deal with impact (ITT): Estimates the impact of being assigned to obtain the coupon, no matter whether or not it was used.
- Native common remedy impact (LATE): Estimates the impact of remedy amongst those that complied with the task — those that used the coupon as a result of they had been assigned to obtain it.
This tutorial introduces the instinct behind these strategies, their assumptions, and the right way to implement them utilizing R (see script here). We may even focus on two-stage least squares (2SLS), the tactic used to estimate LATE.
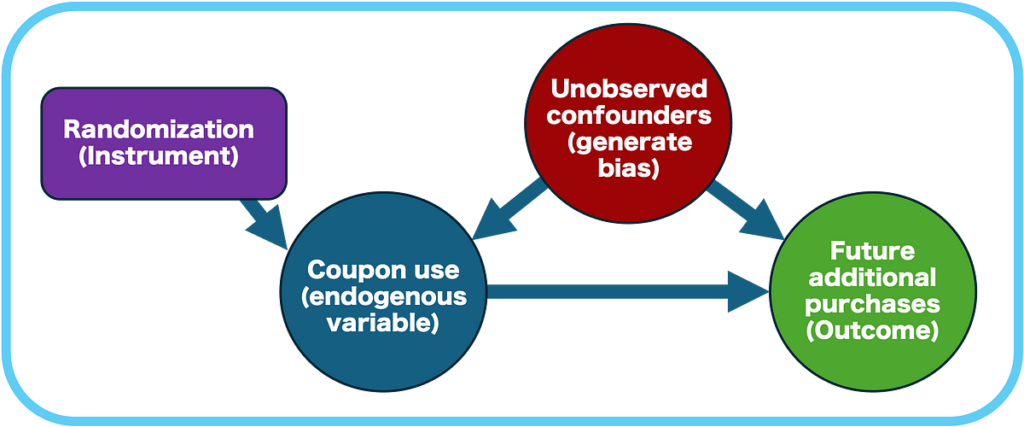
In experiments with imperfect compliance, remedy task (e.g., receiving a coupon) doesn’t completely correspond to consuming the remedy (e.g., utilizing the coupon). So merely evaluating the remedy group to the management group could result in deceptive conclusions, because the impact of the remedy amongst those that took it (the blue group within the determine beneath) will get diluted throughout the bigger remedy group (the inexperienced group).
To take care of this case, we use two foremost approaches:
Intention-to-treat (ITT)
It measures the impact of being assigned to a remedy, no matter whether or not people really observe by with it. In our instance, it compares the long run common purchases of shoppers assigned to obtain a coupon (remedy group) with those that weren’t (management group). This technique is helpful for understanding the impact of the task itself, however it could underestimate the remedy’s impression, because it contains people who didn’t use the coupon.
Native common remedy impact (LATE)
Right here we use the instrumental variables (IV) technique to estimate the native common remedy impact, which is the causal impact of remedy amongst those that complied with the task (“compliers”) — i.e., those that used the coupon as a result of they had been assigned to obtain it. In abstract:
- The random task to remedy (receiving a coupon) is used as an instrumental variable that strongly predicts precise remedy uptake (utilizing the coupon).
- The IV should meet particular assumptions (relevance, exogeneity, and exclusion restriction) that we’ll focus on intimately.
- The IV isolates the a part of variation in coupon use that is attributable to random task, eliminating the affect of unobserved elements that would bias the estimate (see more on “selection bias” here).
- The LATE estimates the impact of remedy by adjusting the impression of remedy task (ITT) for the compliance charge (the chance of utilizing the coupon on condition that the client was assigned).
- It’s estimated through two-stage least squares (2SLS), during which every stage is illustrated within the determine beneath. An intuitive clarification of this technique is mentioned in section 5 here.
Whereas the ITT estimate could be obtained instantly through the use of OLS , IV strategies require robust assumptions to offer legitimate causal estimates. Thankfully, these assumptions are usually met within the experimental situation:
Instrument relevance
The instrumental variable (on this case, task to the remedy group) have to be correlated with the endogenous variable whose impact on future purchases we need to measure (coupon utilization). In different phrases, random task to obtain a coupon ought to considerably enhance the probability {that a} buyer makes use of it. That is examined through the magnitude and statistical significance of the remedy task coefficient within the first stage regression.
Instrument exogeneity and exclusion restriction
The instrumental variable have to be impartial of any unobserved elements that affect the end result (future purchases). It ought to impression the end result solely by its impact on the endogenous variable (coupon utilization).
In less complicated phrases, the instrument ought to affect the end result solely by affecting coupon utilization, and never by every other pathway.
In our situation, the random task of coupons ensures that it isn’t correlated with any unobserved buyer traits that would have an effect on future purchases. Randomization additionally implies that the impression of being assigned a coupon will primarily rely upon whether or not the client chooses to make use of it or not.
Limitations and challenges
- The LATE gives the causal impact just for “compliers” — prospects who used the coupon as a result of they obtained it, and this impact is particular to this group (native validity solely). It can’t be generalized to all prospects or those that used the coupon for different causes.
- When compliance charges are low (which means solely a small proportion of shoppers reply to the remedy), the estimated impact turns into much less exact, and the findings are much less dependable. For the reason that impact is predicated on a small variety of compliers, it is usually tough to find out if the outcomes are significant for the broader inhabitants.
- The assumptions of exogeneity and exclusion restriction aren’t instantly testable, which means that we should depend on the experimental design or on theoretical arguments to assist the validity of the IV implementation.
Now that we perceive the instinct and assumptions, we’ll apply these strategies in an instance to estimate each ITT and LATE in R. We’ll discover the next situation, reproduced on this R script:
An e-commerce firm needs to evaluate whether or not the usage of low cost coupons will increase future buyer purchases. To bypass choice bias, coupons had been randomly despatched to a gaggle of shoppers, however not all recipients used them. Moreover, prospects who didn’t obtain a coupon had no entry to it.
I simulated a dataset representing that state of affairs:
- remedy: Half of the purchasers had been randomly assigned to obtain the coupon (remedy = 1) whereas the opposite half didn’t obtain (remedy = 0).
- coupon_use: Among the many people who obtained remedy, those that used the coupon to make a purchase order are recognized by coupon_use = 1.
- revenue and age: simulated covariates that observe a traditional distribution.
- prob_coupon_use: To make this extra lifelike, the chance of coupon utilization varies amongst those that obtained the coupons. People with increased revenue and decrease age are inclined to have the next probability of utilizing the coupons.
- future_purchases: The result, future purchases in R$, can also be influenced by revenue and age.
- past_purchases: Purchases in R$ from earlier months, earlier than the coupon task. This shouldn’t be correlated with receiving or utilizing a coupon after we management for the covariates.
- Lastly, the simulated impact of coupon utilization for purchasers who used the coupon is ready to “true_effect <- 50“. Which means, on common, utilizing the coupon will increase future purchases by R$50 for many who redeemed it.
Verifying Assumptions
Instrument relevance: The primary stage regression explains the connection between belonging to the remedy group and the utilization of the coupon. On this regression, the coefficient for “remedy” was 0.362, which means that ~36% of the remedy group used the coupon. The p-value for this coefficient was < 0.01, with a t-statistic of 81.2 (substantial), indicating that remedy task (receiving a coupon) considerably influences coupon use.
Instrument exogeneity and exclusion restriction: By building, since task is random, the instrument will not be correlated with unobserved elements that have an effect on future purchases. However in any case, these assumptions are not directly testable through the 2 units of outcomes beneath:
The primary set contains regression outcomes from the primary (only in the script) and second levels (beneath), with and with out covariates. These ought to yield comparable outcomes to assist the concept that our instrument (coupon task) impacts the end result (future purchases) solely by the endogenous variable (coupon use). With out covariates, the estimated impact was 49.24 with a p-value < 0.01, and with covariates, it was 49.31 with a p-value < 0.01.