Quantization
Pushing quantization to its limits by performing it on the function stage with ft-Quantization (ft-Q)
***To know this text, information of embeddings and fundamental quantization is required. The implementation of this algorithm has been launched on GitHub and is totally open-source.
Because the daybreak of LLMs, quantization has turn into one of the fashionable memory-saving strategies for production-ready functions. Not lengthy after, it has been popularized throughout vector databases, which have began utilizing the identical expertise for compressing not solely fashions but additionally vectors for retrieval functions.
On this article, I’ll showcase the restrictions of the present quantization algorithms and suggest a new quantization strategy (ft-Q) to deal with them.
Quantization is a memory-saving algorithm that lets us retailer numbers (each in-memory and in-disk) utilizing a decrease quantity of bits. By default, once we retailer any quantity in reminiscence, we use float32: because of this this quantity is saved utilizing a mix of 32-bits (binary components).
For instance, the integer 40 is saved as follows in a 32-bit object:
Nevertheless, we might determine to retailer the identical quantity utilizing fewer bits (reducing by half the reminiscence utilization), with a 16-bit object:
By quantization, we imply to retailer knowledge utilizing a decrease variety of bits (ex. 32 -> 16, or 32 -> 4), that is also referred to as casting. If we have been to retailer 1GB of numbers (by default saved as 32-bit objects), if we determined to retailer them utilizing 16-bit objects (therefore, making use of a quantization), the dimensions of our knowledge can be halved, leading to 0.5GB.
Is there a catch to quantization?
Saving this quantity of storage seems unimaginable (as you understood, we might preserve reducing till we attain the minimal quantity of bits: 1-bit, also referred to as binary quantization. Our database measurement can be decreased by 32 instances, from 1GB to 31.25MB!), however as you may need already understood, there’s a catch.
Any quantity will be saved as much as the boundaries allowed by all of the attainable combos of bits. With a 32-bit quantization, you’ll be able to retailer a most of 2³² numbers. There are such a lot of attainable combos that we determined to incorporate decimals when utilizing 32-bits. For instance, if we have been so as to add a decimal to our preliminary quantity and retailer 40.12 in 32-bits, it might be utilizing this mix of 1 and 0:
01000010 00100000 01111010 11100001
We have now understood that with a 32-bit storage (given its massive mixture of attainable values) we will just about encode every quantity, together with its decimal factors (to make clear, if you’re new to quantization, the actual quantity and decimal are usually not separated, 40.12 is transformed as a complete into a mix of 32 binary numbers).
If we preserve diminishing the variety of bits, all of the attainable combos diminish exponentially. For instance, 4-bit storage has a restrict of 2⁴ combos: we will solely retailer 16 numbers (this doesn’t go away a lot room to retailer decimals). With 1-bit storage, we will solely retailer a single quantity, both a 1 or a 0.
To place this into context, storing our initials 32-bit numbers into binary code would drive us to transform all our numbers, similar to 40.12 into both 0 or 1. On this state of affairs, this compression doesn’t look superb.
We have now seen how quantization ends in an info loss. So, how can we make use of it, in any case? If you have a look at the quantization of a single quantity (40.12 transformed into 1), it appears there isn’t a worth that may derive from such an excessive stage of quantization, there is just too a lot loss.
Nevertheless, once we apply this system to a set of information similar to vectors, the knowledge loss just isn’t as drastic as when utilized to a single quantity. Vector search is an ideal instance of the place to use quantization in a helpful method.
After we use an encoder, similar to all-MiniLM-L6-v2, we retailer every pattern (which was initially within the type of uncooked textual content) as a vector: a sequence of 384 numbers. The storage of hundreds of thousands of comparable sequences, as you may need understood, is prohibitive, and we will use quantization to considerably diminish the dimensions of the unique vectors by an enormous margin.
Maybe, quantizing our vectors from 32-bit to 16-bit just isn’t this large of a loss. However how about 4-bit and even binary quantization? As a result of our units are comparatively massive (384 numbers every), this appreciable complexity lets us attain the next stage of compression with out leading to extreme retrieval loss.
4-bit quantization
The best way we execute quantization is by wanting on the knowledge distribution of our flattened vector and selecting to map an equal interval with a decrease variety of bits. My favourite instance is 4-bit quantization. With this diploma of complexity, we will retailer 2⁴ = 16 numbers. However, as defined, all of the numbers in our vectors are advanced, every with a number of decimal factors:
array([ 2.43655406e-02, -4.33481708e-02, -1.89688837e-03, -3.76498550e-02,
-8.96364748e-02, 2.96154656e-02, -5.79943173e-02, 1.87652372e-02,
1.87771711e-02, 6.30387887e-02, -3.23972516e-02, -1.46128759e-02,
-3.39277312e-02, -7.04369228e-03, 3.87261175e-02, -5.02494797e-02,
...
-1.03239892e-02, 1.83096472e-02, -1.86534156e-03, 1.44851031e-02,
-6.21072948e-02, -4.46912572e-02, -1.57684386e-02, 8.28376040e-02,
-4.58770394e-02, 1.04658678e-01, 5.53084277e-02, -2.51113791e-02,
4.72703762e-02, -2.41811387e-03, -9.09169838e-02, 1.15215247e-02],
dtype=float32)
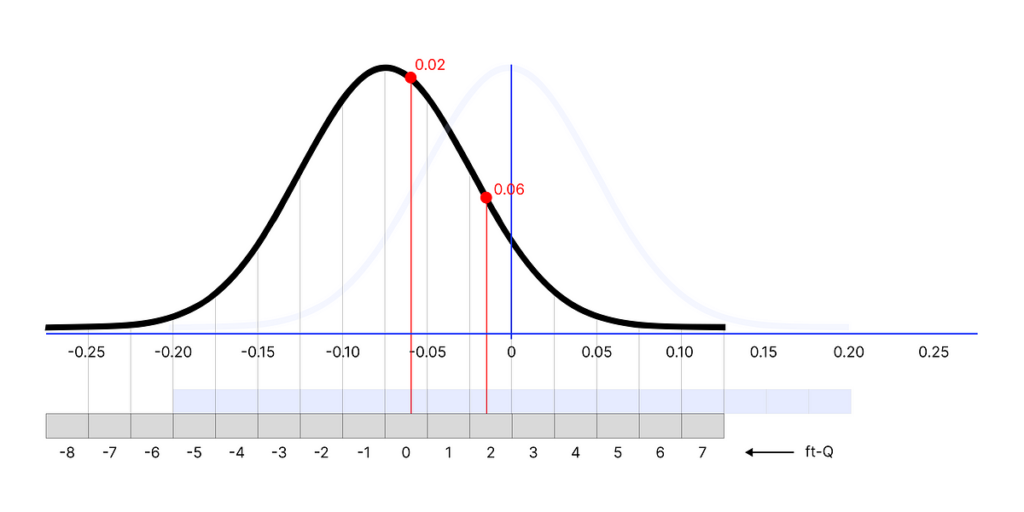
What we will do is map every of our numbers within the distribution into an interval that spans between [-8, 7] (16 attainable numbers). To outline the acute of the interval, we will use the minimal and most values of the distribution we’re quantizing.
For instance, the minimal/most of the distribution is [-0.2, 0.2]. Which means that -0.2 can be transformed to -8, and 0.2 to 7. Every quantity within the distribution could have a quantized equal within the interval (ex. the primary quantity 0.02436554 can be quantized to -1).
array([[-1, -3, -1, ..., 1, -2, -2],
[-6, -1, -2, ..., -2, -2, -3],
[ 0, -2, -4, ..., -1, 1, -2],
...,
[ 3, 0, -5, ..., -5, 7, 0],
[-4, -5, 3, ..., -2, -2, -2],
[-1, 0, -2, ..., -1, 1, -3]], dtype=int4)
1-bit quantization
The identical precept applies to binary quantization however is way easier. The rule is the next: every variety of the distribution < 0 turns into 0, and every quantity > 0 turns into 1.
The principal subject with present quantization strategies is that they reside on the belief that each one our values are based mostly on a single distribution. That’s the reason, once we use thresholds to outline intervals (ex. minimal and most), we solely use a single set derived from the totality of our knowledge (which is modeled on a single distribution).